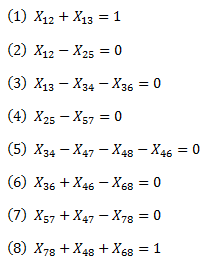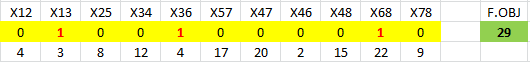El Problema del Camino más Corto (o ruta más barata) consiste en encontrar una ruta o camino óptimo entre un nodo fuente y un nodo destino, los cuales están enlazados a través de una red con arcos que poseen un cierto atributo, el cual puede ser costo, distancia, tiempo, etc.
La Programación Entera permite abordar de forma eficiente este tipo de problemas, en especial cuando la cantidad de nodos y rutas posibles resulta ser un número significativo. Utilizar en estos casos un enfoque intuitivo de resolución es tedioso y de no ser exhaustivo no garantiza la identificación de la mejor alternativa o ruta.
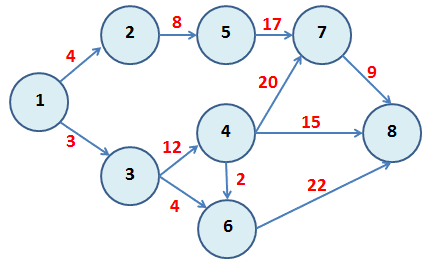
Consideremos el siguiente diagrama donde los números asignados a cada uno de los arcos representan la distancia en kilómetros de un nodo a otro. Se desea encontrar la ruta con la distancia mínima para ir del nodo 1 al nodo 8.
El tamaño reducido de la red anterior permite encontrar el camino más corto simplemente enumerando las distintas alternativas que comenzando en el nodo 1 permita llegar al nodo 8. De esta forma las rutas posibles son:
- Ruta 1-2-5-7-8: 4+8+17+9=38[km]
- Ruta 1-3-4-7-8: 3+12+20+9=44[km]
- Ruta 1-3-4-6-8: 3+12+2+22=39[km]
- Ruta 1-3-4-8: 3+12+15=30[km]
- Ruta 1-3-6-8: 3+4+22=29[km]
La ruta o camino más corto esta dada por la secuencia 1-3-6-8 con una distancia total de 29[km].
A continuación se formula un modelo de Programación Entera que permite extender este tipo de resultados a un problema de estas características:
Variables de Decisión:
Función Objetivo: Minimizar la distancia total en [km] dada por la siguiente expresión:
Restricciones:
- La primera restricción (1) garantiza que sólo un nodo (entre el 2 y el 3) pueda ser el que se visita a continuación de comenzar en el nodo 1.
- La restricción (2) determina que si se visito el nodo 2 después del nodo 1, entonces necesariamente el nodo 5 será visitado después del nodo 2.
- La restricción (3) permite verificar que si el nodo 3 fue visitado luego del nodo 1, entonces a continuación se visita el nodo 4 o el nodo 6 (sólo uno de ellos).
- La restricción (4) establece que si el nodo 5 fue visitado luego del nodo 2, entonces el nodo 7 debe ser visitado luego del nodo 5.
- La restricción (5) garantiza que si el nodo 4 fue visitado luego del nodo 3, entonces a continuación se visita uno de los siguientes nodo: 7, 8 o 6.
- La restricción (6) indica que si el nodo 6 fue visitado inmediatamente luego de estar en el nodo 3 o 4, a continuación se visita el nodo 8.
- La restricción (7) determina que si el nodo 7 fue visitado inmediatamente luego de estar en el nodo 4 o 5, a continuación se visita el nodo 8.
- Finalmente la restricción (8) asegura que ya sea el nodo 7, 4 o 6 sea el último en visitar previo a terminar la ruta en el nodo 8.
Al implementar en Solver el problema del Camino más Corto o Ruta Mínima anterior se alcanzan los siguientes resultados:
Donde se corrobora que la ruta más corta (solución óptima) corresponde al camino 1-3-6-8 con una distancia total de 29[km] (valor óptimo).
Método Dijkstra:
El Algortimo de Dijkstra, también denominado Algoritmo de caminos mínimos, es un modelo que se clasifica dentro de los algoritmos de búsqueda. Su objetivo, es determinar la ruta más corta, desde el nodo origen, hasta cualquier nodo de la red. Su metodología se basa en iteraciones, de manera tal que en la práctica, su desarrollo se dificulta a medida que el tamaño de la red aumenta, dejándolo en clara desventaja, frente a métodos de optimización basados en programación matemática.
¿Qué tipos de redes pueden resolverse por medio del Algoritmo de Dijkstra?
Este algoritmo, al igual que el método de Floyd, tienen la capacidad de resolver el problema de la ruta más corta, tanto para redes cíclicas, como para redes acíclicas. De manera tal que los bucles que presente una red, no restringen el uso del algoritmo.
El algoritmo de Dijkstra hace uso y define etiquetas a partir del nodo origen y para cada uno de los nodos subsiguientes. Estas etiquetas contienen información relacionada con un valor acumulado del tamaño de los arcos y con la procedencia más próxima de la ruta.
Las etiquetas corresponden a los nodos, no a los arcos. En el algoritmo de Dijkstra, estas etiquetas son temporales y permanentes. Las etiquetas temporales son aquellas que son susceptibles de modificarse mientras exista la posibilidad de hallar para sí, una ruta más corta; de lo contrario, dicha etiqueta pasa a ser permanente.
Etiqueta = [acumulado, nodo procedente] iteración
Algoritmo de Dijkstra - Ejemplo
Teniendo en cuenta la siguiente red, que tiene como origen el nodo 1:

Procedemos con las iteraciones, partimos de la iteración 0, es decir, asignar la etiqueta para el nodo origen:
Iteración 0
En este paso, asignamos una etiqueta permanente para el nodo origen. Recordemos que la etiqueta se compone por un valor acumulado, que en este caso debe ser 0, ya que es el punto base y que no existe procedencia:
Etiqueta nodo 1 = [valor acumulado, procedencia] iteración
Etiqueta nodo 1 = [0, -] 0
Iteración 1
En este paso, evaluamos a cuáles nodos se puede llegar desde el nodo 1. En este caso se puede llegar a los nodos 2 y 3. De manera que debemos asignar las etiquetas para cada nodo:
Etiqueta nodo 2 = [valor acumulado, procedencia] iteración
Etiqueta nodo 2 = [0 + 100, 1] 1
0 es el valor acumulado en la etiqueta del nodo de procedencia, en este caso el valor acumulado para el nodo 1. 100 es el valor del arco que une el nodo procedencia (1) y el nodo destino (2). 1 es el número de la iteración.
Etiqueta nodo 3 = [valor acumulado, procedencia] iteración
Etiqueta nodo 3 = [0 + 30, 1] 1
En este caso, podemos observar que la etiqueta del nodo 3, ya contiene el menor valor acumulado posible para llegar a este. Ya que 30 es la mínima distancia posible, toda vez que para llegar al nodo 3 por medio del nodo 2, tendrá que recorrer como mínimo el valor absoluto del arco que une el origen con el nodo 2 = 100. Así entonces, la etiqueta del nodo 3 pasa a ser permanente.
Tabulamos la iteración 1:


Iteración 2:
En este paso, evaluamos las posibles salidas desde el nodo 3, es decir los nodos 4 y 5. De manera que debemos asignar las etiquetas para cada nodo:
Etiqueta nodo 4 = [valor acumulado, procedencia] iteración
Etiqueta nodo 4 = [30 + 10, 3] 2
Etiqueta nodo 4 = [40, 3] 2
30 es el valor acumulado en la etiqueta del nodo de procedencia, en este caso el valor acumulado para el nodo 3. 10 es el valor del arco que une el nodo procedencia (3) y el nodo destino (4). 2 es el número de la iteración.
Etiqueta nodo 5 = [valor acumulado, procedencia] iteración
Etiqueta nodo 5 = [30 + 60, 3] 2
Etiqueta nodo 4 = [90, 3] 2
30 es el valor acumulado en la etiqueta del nodo de procedencia, en este caso el valor acumulado para el nodo 3. 60 es el valor del arco que une el nodo procedencia (3) y el nodo destino (5). 2 es el número de la iteración.
En este caso, podemos observar que la etiqueta del nodo 4, contiene el menor valor acumulado posible para llegar a este. Así entonces, la etiqueta del nodo 4 pasa a ser permanente.
Tabulamos la iteración 2:


Iteración 3:
En este paso, evaluamos las posibles salidas desde el nodo 4, es decir los nodos 2 y 5. De manera que debemos asignar las etiquetas para cada nodo:
Etiqueta nodo 2 = [valor acumulado, procedencia] iteración
Etiqueta nodo 2 = [40 + 15, 4] 3
Etiqueta nodo 2 = [55, 4] 3
40 es el valor acumulado en la etiqueta del nodo de procedencia, en este caso el valor acumulado para el nodo 4. 15 es el valor del arco que une el nodo procedencia (4) y el nodo destino (2). 3 es el número de la iteración.
Etiqueta nodo 5 = [valor acumulado, procedencia] iteración
Etiqueta nodo 5 = [40 + 50, 4] 3
Etiqueta nodo 5 = [90, 4] 3
40 es el valor acumulado en la etiqueta del nodo de procedencia, en este caso el valor acumulado para el nodo 3. 50 es el valor del arco que une el nodo procedencia (4) y el nodo destino (5). 3 es el número de la iteración.
En este caso, podemos observar que el nodo 2 ahora cuenta con 2 etiquetas temporales, y definitivas, ya que no existe otra ruta hacia dicho nodo. De manera que se elige la etiqueta que tenga el menor valor acumulado. Así entonces, la etiqueta del nodo 2 con procedencia del nodo 4, pasa a ser permanente.
Tabulamos la iteración 3:


Iteración 4:
En este paso, evaluamos las posibles salidas desde el nodo 2 y el nodo 5. Sin embargo, el nodo 2 solo tiene un posible destino, el nodo 3, el cual ya tiene una etiqueta permanente, de manera que no puede ser reetiquetado. Ahora, evaluamos el nodo 5 y es un nodo que no tiene destinos. Así entonces, su etiqueta temporal pasa a ser permanente, en este caso cuenta con 2 etiquetas que tienen el mismo valor, es decir, alternativas óptimas. De esta manera concluye el algoritmo de Dijkstra.

¿Cuál es la ruta más corta?
La ruta más corta entre el nodo 1 (origen) y cualquier otro nodo de la red (destino), se determina partiendo desde el nodo destino y recorriendo las procedencias de sus etiquetas. Por ejemplo:
¿Cuál es la ruta más corta entre el nodo 1 y el nodo 4?
En este caso, debemos partir desde la etiqueta del nodo 4.


La ruta más corta entre el nodo 1 y el nodo 4 tiene un valor acumulado de: 40
Es necesario considerar, que los valores utilizados en los arcos de la red objeto de estudio del algoritmo de Dijkstra, no necesariamente representan distancias. Si bien, es un modelo que aborda el denominado "problema de la ruta más corta"; en la práctica, puede utilizarse para optimizar: distancia, costos, tiempo.
De hecho, los sistemas de ruteo utilizados en la actualidad, priorizan los costos y el tiempo como variable decisión de los modelos de optimización.